| |
The unit vector 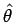 is perpendicular to OP in the direction of increasing is perpendicular to OP in the direction of increasing 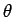 . The angle that . The angle that 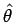 makes with the positive z-axis is makes with the positive z-axis is 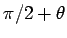 . . |
| |
Substituting for 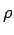 , we get , we get |
| |
The azimuthal unit vector 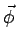 is in the direction of increasing angle is in the direction of increasing angle 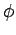 . It is perpendicular to . It is perpendicular to 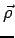 and has no z- component. It can be easily seen that and has no z- component. It can be easily seen that |