In view of the spherical symmetry of the atom, it is more convenient to use spherical coordinates( 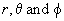) rather than Cartesian coordinates
(x, y, z) in the description of the system. The relation between the spherical and Cartesian coordinates is illustrated in Figure 4.1
Figure 4.1 Cartesian and spherical polar coordinate systems
The solution to (4.1) can be written as the product of a radial part R and an angular part . The angular part can further be written as a product of two functions, one, of thet polar angle and the other of the azimuthal angle.
(4.2)
Equation 4.1 cannot be separated into three equations in which each equation depends on x or y or z. Such a separation was possible for a particle in a box wherein the potential V was zero. In the hydrogen, atom, the potential depends only on r. Therefore, the Schrodinger Equation 4.1 takes the following form in terms of the variables .
) rather than Cartesian coordinates
(x, y, z) in the description of the system. The relation between the spherical and Cartesian coordinates is illustrated in Figure 4.1 
. The angular part can further be written as a product of two functions, one, of thet polar angle and the other of the azimuthal angle. 
