Population of the band energy levels by electrons.
In our earlier section on bands (with N electrons) in metals, we saw that only N / 2 levels were doubly occupied at T = 0 . The highest occupied MO (HOMO) was called the Fermi level. At temperatures other than T = 0, the occupation of levels does not follow the Boltzmann probability distribution p(Ei) 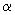e -Ei / kBT but follows the Fermi Dirac distribution which is given by
p(Ei) = 1/ [e (Ei-
) / kBT +1]
(20.17)
Here,
is the value of Ei for which p ( Ei ) = 1/ 2. is called the chemical potential. The Fermi-Dirac distribution includes the effect of the Pauli exclusion principle, according to which no two electrons can have all quantum numbers identical; i.e., for each state ( or non-degenerate level ), there can be at most one electron of a given spin type. For energies close to and less than eq (20.17) differs completely from the Boltzmann distribution. For energies greater than and for large T, the second term of the denominator of (20.17) is very small and P ( Ei ) resembles the Boltzmann distribution
p (Ei) = e - (Ei - ) / kBT
(20.18)
A sketch of P(Ei) vs (Ei - ) / is given in fig 20.8
Figure 20.8 Population of electronic energy levels according to Fermi-Dirac distribution.
The curves are labeled by ... ..... / kBT. The distribution at T = 0 is the shaded region where p (Ei) = 1 for Ei< and 0 otherwise.
e -Ei / kBT but follows the Fermi Dirac distribution which is given by 
) / kBT +1] 
is the value of Ei for which p ( Ei ) = 1/ 2. 
