A simplified picture of the periodic potential is given in Fig. 3.5
It is quite similar to the finite potential analysis
periodicity = a + b 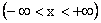
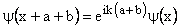 , where k is continuous , where k is continuous
We will first consider the case: 0 < E < U 0
Inside well wave function = 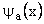
Outside well wave function = 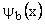
Schrödinger equation for 0 < x < a:
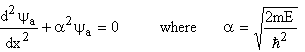 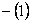
Schrödinger equation for -b < x < 0:
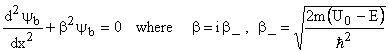 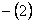
The general solutions to equations (1) and (2) are:
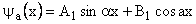
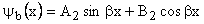
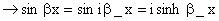
Now applying the continuity condition on wave function and its derivative at x = 0
Fig. 3.6
continuity requirement
Note that x = -b is the same boundary as that of x = a.
Now wave function and its derivative must observe Bloch Theorem
With
periodicity requirements.
Applying Boundary and Periodicity conditions
Eliminating 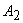 and and 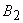 by using first two equations in last two equations by using first two equations in last two equations
 2 eqns in 2 unknown constants. For non trivial values of 2 eqns in 2 unknown constants. For non trivial values of 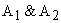 , the determinant formed from coefficient should be equal to zero. , the determinant formed from coefficient should be equal to zero.
|