Bloch Theorem

Relates value of wave function within any unit cell of a periodic potential to an equivalent point in any other unit cell.

Concentrate on the behavior of any unit cell in the whole array. For 1D system the Bloch theorem says that if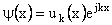

(1) if U(x) is the periodic such that U(x + a) = U(x)

then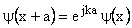

(2) Equivalently,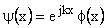

where = wave function for an unit cell. and

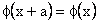
Boundary conditions are imposed at end points of the periodic potential.

Now, the wave number k in periodic potential set has several properties as:

.  It can be shown that and only two distinct values of k exist for each and every allowed values of E i.e. .

.  For a given E, values of k differing by a multiple of give rise to one and same wave function solution. As k is periodic or multiple-valued with a range . Usually we take range .

.  If the periodic potential is assumed to be in extent, running from to then there are restrictions on k. k can take a continumm of values. k must be real otherwise exp(jkx) or thus will blow up at either or .

.  In dealing with crystals of finite extent, information about the boundary conditions on crystal surface may be lacking. To avoid this we assume a periodic boundary condition assuming the lattice is a ring of N atoms.

Therefore,    or

So for the 1D lattice of ions the periodic set of finite potential wells, for large array x may be assumed to go from .

Thus for a finite crystal k can only assume a set of discrete values, but as N is large therefore one has closely spaced discrete values.