P-N junction Diodes
Abrupt p-n junction
Fig.10.3
Built-in potential= 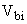
At equilibrium 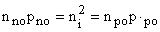
Thus
Thus 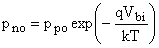 minority carrier in n side minority carrier in n side
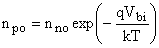 minority carrier in p side minority carrier in p side
Thermal equilibrium E field in neutral regions=0
Thus Total-ve charge in P side-total + ve charge in n side
Fig.11.4
Poissons Equation 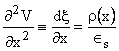
In n side 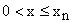
.
Integrating
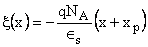 for for 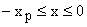
|
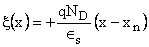 for for 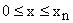
|
Maxwell's field at x=0(junction) 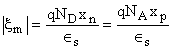
Also we obtain 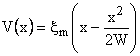
W=Total depletion region width
Eliminating 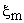 from previous 3 equations. from previous 3 equations.
More accurate expression for depletion region width
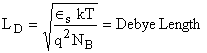 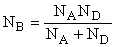
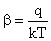 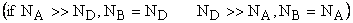 If one side is heavily doped the depletion region is in weakly doped place) Depletion -layer capacitance per unit area If one side is heavily doped the depletion region is in weakly doped place) Depletion -layer capacitance per unit area
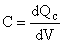 , , 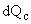 Incremental increase in charge per unit area for a voltage increase of Incremental increase in charge per unit area for a voltage increase of
Inside depletion layer assuming the following
. Boltzman relation is an approximation
. Abrupt Depletion Layer
. Low injection (injected minority carrier < majority carrier)
. No generation current inside depletion layer
where 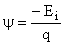 and and 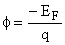
When voltage is applied the minority carrier densities on both sides are changed and 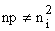
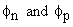 are imrefs or quasi Fermi level for electrons and holes (E Fn and E Fp ) under nonequilibrium are imrefs or quasi Fermi level for electrons and holes (E Fn and E Fp ) under nonequilibrium  condition as applied voltage/bias or optical field as shown in Fig. 10.4 condition as applied voltage/bias or optical field as shown in Fig. 10.4
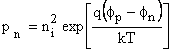 ....... ....... 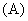
|
Forward bias 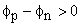 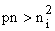
Reversed bias 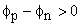 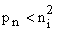
Now 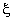 = = 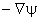
Similarly
Electron and hole current densities is proportional to gradient of quasi Fermi level.
Now  applied voltage across the junction. Now at the boundary of depletion layer at p side i.e. at applied voltage across the junction. Now at the boundary of depletion layer at p side i.e. at
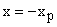 We have from (A) & (B) We have from (A) & (B)
Where 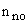 is the equilibrium electron density on the p side. is the equilibrium electron density on the p side.
Similarly 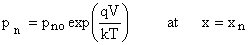 |
Where 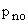 is the equilibrium hole density on the p side. is the equilibrium hole density on the p side.
n side Continuity equation in steady state
Let 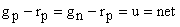 recombination rate recombination rate
Then in 1-D we obtain
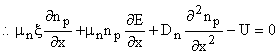 (steady state) (steady state)
|
for n side 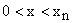
Charge neutrality holds approximately
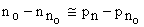
ultiplying first by 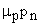 and second equation by and second equation by 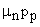 and taking Einstein relation as and taking Einstein relation as 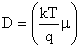
we get 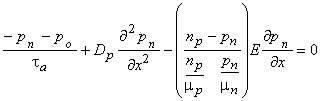 |
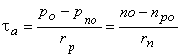 =lifetime =lifetime
|
as 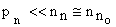 in n-type in n-type |
Low injection assumption 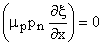 |
Neutral region 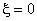
Now Boundary condition 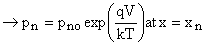 (injection) (injection)
assuming large structure
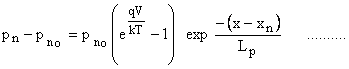 exponential decay of electron and hole current components in the Depletion region as shown in Fig. 10.5 exponential decay of electron and hole current components in the Depletion region as shown in Fig. 10.5
|