Quantum mechanics
To extend Bohr theory to He, Li, we need Quantum Mechanics which requires
Wave Particle Duality of De Broglie
Total energy 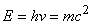 , where m is the mass of a photon. , where m is the mass of a photon.
Therefore, photon mass = 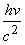 and and
Photon momentum 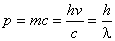 . .
Therefore an argument could be made that an electron with a mass 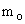 and momentum also has a wavelength , and can then and momentum also has a wavelength , and can then
be represented by wave, where for this particle momentum p can be associated with a wave of wavelength 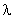 , where particle momentum , where particle momentum 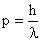
Schrödinger and Heisenberg  quantum mechanics to describe small particles like electrons, etc. quantum mechanics to describe small particles like electrons, etc.
Postulates of Quantum Mechanics
. There exist a wave function 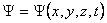 of a particle where x, y and z are the space variables and t is the time. From this of a particle where x, y and z are the space variables and t is the time. From this 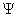 one can find the dynamic behaviour of a particle in system, one can find the dynamic behaviour of a particle in system, 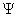 is complex. is complex.
. The 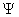 for a given system is determined by Schrödinger equation: for a given system is determined by Schrödinger equation:
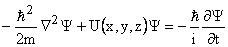 , where m is the mass of the particle and , where m is the mass of the particle and 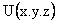 is the potential energy operator for the system. is the potential energy operator for the system.
. 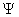 and and 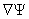 must be finite, continuous and single-valued for all x, y, z and t. must be finite, continuous and single-valued for all x, y, z and t.
. 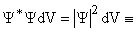 probability that the particle is in a spatial volume element dV. So, probability that the particle is in a spatial volume element dV. So, 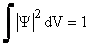 , integration over all space. , integration over all space.
. A mathematical operator 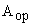 can be associated with each dynamic system variable i.e. position, momentum, velocity, etc. can be associated with each dynamic system variable i.e. position, momentum, velocity, etc.
The expectation value, when this operator operates on 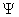 is given as is given as
As examples, the space variables x, y, z are given as
The momentum 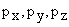 are given as are given as
where 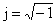
Similarly
Energy E is derived with an operator 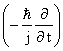
Therefore the expected value of energy from postulate 5 is
If energy = E 0 (constant) 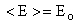
or
or
|