Histogram Equalization

The goal is to obtain a uniform histogram for the output image.

Consider the transformation function

	(5.1)

where w is dummy variable of . The RHS of above equation represents the cumulative distribution function (CDF) of r The two conditions set forth for T(r ) are satisfied since CDF increases monotonically from 0 to 1 as a function of r

Substitution for in we have, = 1,

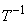
which is a uniform density in the interval of definition of the transformed variable s . Note also that this result is independent of the inverse transformation function ( ). This is important because it is not always easy to obtain for image analysis.

This transformation in terms of enhancement implies an increase in the dynamic range of the pixels which can have a considerable effect in the appearance of an image.

We have,

To show: is in fact uniform.

Since r lies in [0,1]

,

whish is a uniform density function in the desired image.

(continued in the next slide)