Image Enhancement by histogram modification
The histogram of an image represents the relative frequency of occurrence of the various gray levels in the image.
It provides a total description of the appearance of an image. The type and degree of enhancement obtained depends on the nature of the specified histogram.
Let the variable r represent the grey level of the pixels in the image to be enhanced. Assume that the pixel values are normalized to lie in the range
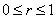 with with 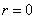 represents black represents black
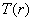 represents white in the gray scale represents white in the gray scale
For any r in [ 0,1 ], we consider transformations of the form 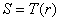 which produce a level S for every pixel value r in the original image. It is assumed that the transformation function satisfies the conditions: which produce a level S for every pixel value r in the original image. It is assumed that the transformation function satisfies the conditions:
(1)
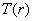 ) is singled valued and monotonically increasing in the interval { ) is singled valued and monotonically increasing in the interval { 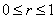 }; };
(2) 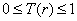 , for , for 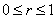
Condition (1) transformation preserves the order from black to white in the gray scale
Condition (2) transformation guarantees a mapping that is consistent with the allowed range of pixel values.
Example of such a transformation is:
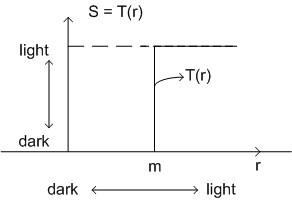
Figure( 5.2) |
The inverse transform 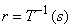 for for 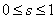 , where it is assumed , where it is assumed 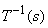 satisfies conditions (1) or (2) wrt variables The gray levels in an image are random quantities in the interval [0,1] . Assuming that they are continuous variables the original and transformed gray levels can be characterized by their probability density functions Pr(r) and Ps(s ). A great deal can be said about the general characteristics of an image from the density functions of its gray levels. satisfies conditions (1) or (2) wrt variables The gray levels in an image are random quantities in the interval [0,1] . Assuming that they are continuous variables the original and transformed gray levels can be characterized by their probability density functions Pr(r) and Ps(s ). A great deal can be said about the general characteristics of an image from the density functions of its gray levels.
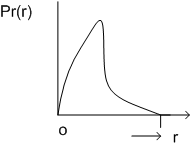
Figure 5.3a This function implies that the image will have dark characters since majority of levels are concentrated inthe dark region of gray scale |
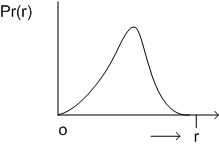
Figure 5.3b
The image will have predominant light tones since majority of pixels are light gray. |
It follows from elementary probability theory that if Pr(r) and 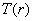 are known and are known and 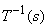 satisfies condition (1), then satisfies condition (1), then
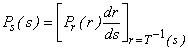
The enhancement techniques are based on modifying the appearance of an image by controlling the probability density function of its gray levels via the transformation function 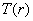 . .
|