Effect of sampling in frequency
Let 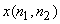 be a general signal with Fourier transform be a general signal with Fourier transform 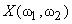 , then we can sample it as in eqn (4.2.5). If we then take the IDFT of the function , then we can sample it as in eqn (4.2.5). If we then take the IDFT of the function 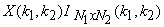 , we obtain the signal , we obtain the signal 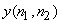 , ,

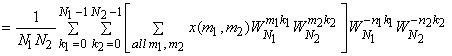 |
(4.2.7) |
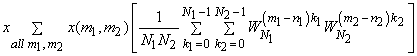 |
(4.2.8) |
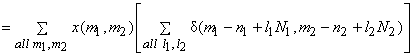 |
(4.2.9) |
which displays spatial domain aliasing caused by sampling in frequency. If the original signal x had a finite support  and we took dense enough samples of its Fourier transform, satisfying and we took dense enough samples of its Fourier transform, satisfying 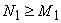 and and 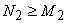 then, we would have no overlap in (4.2.10) or equivalently. then, we would have no overlap in (4.2.10) or equivalently.
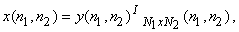
and will have avoided the aliased terms from coming into this spatial support region. One interpretation of (4.2.6) is taken as a numerical approximation to the inverse FT (IFT) whose exact form is not computationally feasible. We thus see that the substitution of an IDFT for the IFT can result in spatial domain aliasing, which, however, can be controlled by taking the uniformly spaced samples at high enough rates to avoid significant (or any) spatial overlap (alias).
|