Relation of DFT to Fourier Transform
For a finite support sequence, x, we compare both the Fourier transform 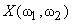 as well as the DFT as well as the DFT 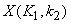 . We now answer the question of the relation of these two. Comparing, we have . We now answer the question of the relation of these two. Comparing, we have
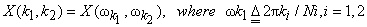 |
(4.2.5) |
for
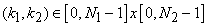 . This means that the central or primary period of the Fourier transform . This means that the central or primary period of the Fourier transform 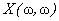 is not what is sampled, but rather an area of equal size in its first quadrant. Of course, by periodicity this is equivalent to sampling in the primary period. Based on such considerations, we can construct the diagram of Figure (4.5) indicating where the DFT samples come from in the Fourier transform plane. In particular, all the FT samples along the is not what is sampled, but rather an area of equal size in its first quadrant. Of course, by periodicity this is equivalent to sampling in the primary period. Based on such considerations, we can construct the diagram of Figure (4.5) indicating where the DFT samples come from in the Fourier transform plane. In particular, all the FT samples along the 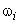 axes map into axes map into 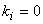 in the DFT, and the possible samples (they occur only for Ni even) at in the DFT, and the possible samples (they occur only for Ni even) at 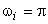 map into map into 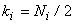 . Also note the indicated mapping of the four quadrants of . Also note the indicated mapping of the four quadrants of
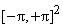 in the in the
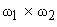 plane onto plane onto 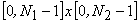 in the first quadrant of the in the first quadrant of the
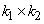 plane. plane.
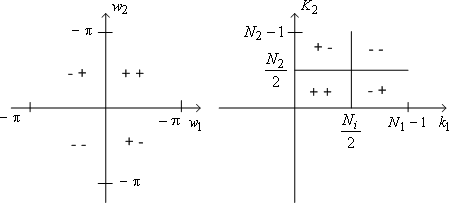
Figure (4.5): Mapping of FT samples to DFT locations
|
Example (DFT symmetry in real-valued signal case)
When the image (Signal) is real valued, we have the following DFT symmetry property
When the DFT is stored, we only need to consider the locations
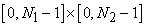 . For these locations, we can then write . For these locations, we can then write
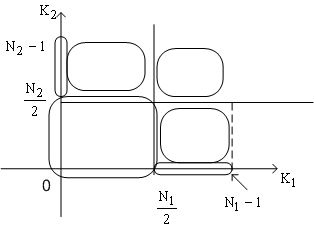
Figure (4.6):Illustration of conjugate symmetry in DFT storage for real-valued image data. |
This then gives us the conjugate symmetry through the point
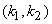 = =
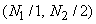 as shown in figure (4.6 ). The big square with round corners shows an essential part of the DFT coefficients and comprises locations as shown in figure (4.6 ). The big square with round corners shows an essential part of the DFT coefficients and comprises locations 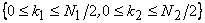 . .
The other essential part is one of the two smaller round-cornered squares that share a side with this large square-for example, the upper square, which comprises points 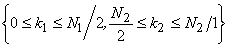 . The other smaller square are not needed by the symmetry condition above. Neither are the two narrow regions along the axes. Such symmetry can be used to reduce storage by approximately one-half. We need only to store the coefficients for the resulting nonsymmetrical half-size region. . The other smaller square are not needed by the symmetry condition above. Neither are the two narrow regions along the axes. Such symmetry can be used to reduce storage by approximately one-half. We need only to store the coefficients for the resulting nonsymmetrical half-size region. |