DFT Properties(cont.)
• Parseval's theorem:
With special case for x=y, the "energy balance formula," since the left-hand side then becomes the energy of the signal

• Symmetry properties:
(a) Conjugation:
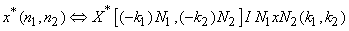
(b) Arguments reversed (modulo reflection through origin):
(c) Real-valued sequences (special case):
By the conjugation property above, applying it to a real-valued sequence 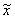 , we have the conjugate symmetry property , we have the conjugate symmetry property
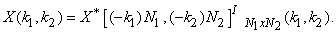 |
(4.2.4) |
From this equation, the following four properties follow easily:
i) 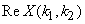 is even, i.e., is even, i.e., 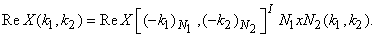
ii) Im 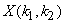 is odd, i.e. is odd, i.e.
Im 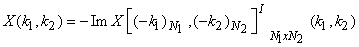 . .
iii) 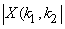 is even, i.e., is even, i.e.,
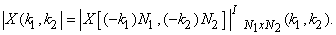
iv) arg 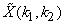 is odd, i.e., is odd, i.e.,
arg 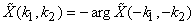
These last properties are used for reducing required data storage for the DFT by an approximate factor of ½ in the real-valued image case.
|