DFT Properties
The properties of the DFT are similar to those of the discrete Fourier series. The key difference is that the support of the sequence x and of the DFT X is finite. We consider two sequences x and y with the same rectangular 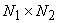 support, having DFT transforms X and Y, respectively. We then offer proofs of some of these properties below. support, having DFT transforms X and Y, respectively. We then offer proofs of some of these properties below.
• Linearity:
when both sequences have the same support

• Circular convolution : We define circular convolution for two finite support sequences with the same period as
 |
(4.2.3) |
Using the operator symbol  . We then the following transform pair: . We then the following transform pair:
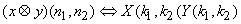 . .
• Multiplication:
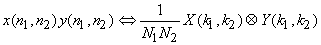 . .
• Separability:
 , ,
the separable product of a 1-D N1 -point and N2 -point DFT.
• Circular shifting: 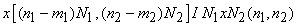
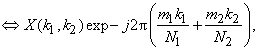 where the shift vector where the shift vector 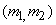 is integer valued. is integer valued. |