Major advantages
Example 2: Vector quantisation can also exploit non linear dependence. Consider two random variables f1 and f2 whose joint pdf 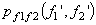 is shown in Figure (3.4.6). The pdf is uniform with amplitude 1/(8a2) in the shaded region and '0' outside the shaded region. The marginal density functions is shown in Figure (3.4.6). The pdf is uniform with amplitude 1/(8a2) in the shaded region and '0' outside the shaded region. The marginal density functions 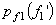 and and 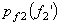 are also shown. are also shown. 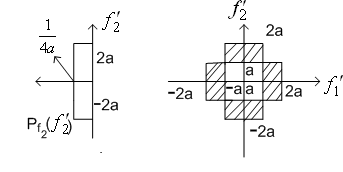
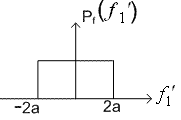
Figure( 3.4.6)
From the joint 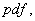 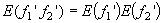 . .
.This implies f1 and f2 are linearly independent. However 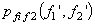 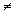 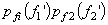
Therefore f1 and f2 are statistically dependent. When the random variables are linearly independent and statistically dependent, they are said to be nonlinearly dependent. If we quantise f1 and f2 separately, using the MSE criterion, and allow two reconstruction levels for each of f1 and f2, the optimal reconstruction levels for each scalar are 'a' and -a.
The average distortion 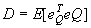 is a2/2. is a2/2. The resulting reconstruction levels in this case are the four filled-in dots shown in Figure(3.4.7).
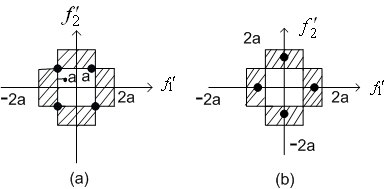
Figure (3.4.7)
Using vector quantisation, we can choose the four reconstruction levels as shown in Figure ( 3.4.7). The average distortion D=5a2/12.This example shows that using vector quantisation can reduce the MSE without increasing the number of reconstruction levels.
Linear transformation can always eliminate linear dependence. The nonlinear dependence can be eliminated using an invertible nonlinear operation. If we eliminate linear or non linear dependence prior to quantization, then the advantage that vector quantisation derives from exploiting linear or non linear dependence will disappear.
|