Major advantages

1.      Vector Quantization can lower the average distortion D with number of reconstruction levels held constant; or,

2.      Can reduce the number of reconstruction levels when D is held constant.

The most significant way vector quantization can improve performance over scalar quantization is by exploiting the statistical dependence among scalars in the block. Let us consider two examples.

Example 1: In this example, we consider the exploitation of linear dependence (correlation). Consider two random variables f₁ and f₂ with a joint probability density function (pdf) shown in Figure (3.4.2). The pdf is uniform with amplitude 1/2a² in shaded region and zero in unshaded region.

  The probability density function is uniform with amplitude 1/2a² in the shaded region and zero in the unshaded region. The marginal probability density function's and are:

Figure( 3.4.3)

Since , are correlated or linearly dependent. Suppose we quantize f₁  and 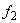separately using scalar quantization and MMSE criterion.

Since each of the two scalars has a uniform probability density function, the optimal quantizer is a uniform quantizer. If we allow 2 reconstruction levels for each scalar as,

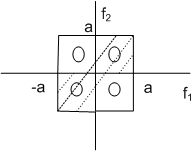
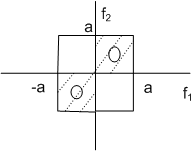
Fig (3.4.4)

the optimal reconstruction levels for each scalar are a/2 and -a/2. The resulting four reconstruction levels are shown in Fig (3.4.4 ). Clearly 2 of the 4 reconstruction levels are wasted. With VQ we can reduce the number of reconstruction levels to 2 without sacrificing MSE  as shown in Fig (3.4.4) This example shows that vector quantisation can reduce the number of reconstruction levels without sacrificing the MSE.

              We can eliminate the linear dependence between f₁ and f₂ in this example by rotating the pdf clockwise by 45⁰, as as shown in Figure (3.4.5).

In the new coordinate system, g₁ and g₂ are uncorrelated i.e.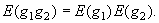

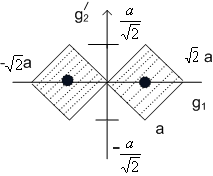
Figure( 3.4.5)

In this new coordinate system, it is possible to place the two reconstruction levels at the filled-in dots shown in the figure by scalar quantisation of the two scalars, and the advantage of vector quantisation disappears. Hence, eliminating the linear dependence reduces the advantage of vector quantization in this example. This is consistent with the notion that vector quantisation can exploit linear dependence of the scalars in the vector.