Periodic Sampling with Arbitrary Sampling Geometries:
We define two linearly independent vectors
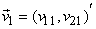 and and
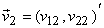 and write the locations of a doubly periodic set of samples in and write the locations of a doubly periodic set of samples in
 -pl as -pl as
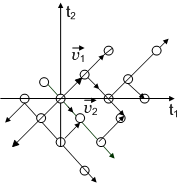
Figure( 3.2.1)
|
Using vector notation we express these relations as
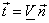 where where
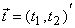 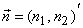 is an integer indexing vector with is an integer indexing vector with 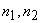 as unitless coordinate variables and as unitless coordinate variables and
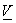 is a matrix made up of the sampling vectors is a matrix made up of the sampling vectors
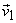 and and
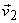 i.e i.e
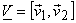 . .
As
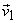 and and
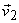 are linearly independent, the determinant of are linearly independent, the determinant of 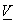 is non-zero. We refer to is non-zero. We refer to
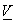 as the sampling matrix . The basis vectors can be interpreted as columns of as the sampling matrix . The basis vectors can be interpreted as columns of 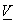 which maps index values to actual sampling positions of a spatially continuous signal. Sampling a continuous signal which maps index values to actual sampling positions of a spatially continuous signal. Sampling a continuous signal
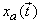 produces the discrete signal produces the discrete signal
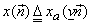 .The sampling locations are shown in Fig (3.2.1). .The sampling locations are shown in Fig (3.2.1).
At this stage we ask the questions,
1) How are the FT's of
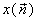 and and
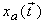 related? related?
2)
Under what circumstances can we reconstruct
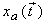 from its samples from its samples
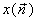 ? ?
We proceed by defining the 2D-FT of
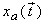 as: as:
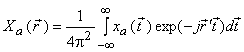
where
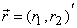 and and 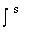 are double integrals, because are double integrals, because  and and 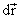 are vectors respectively. are vectors respectively.
The discrete time FT i.e. (DTFT) of 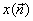 can be written as can be written as
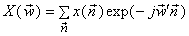
where 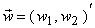 and and
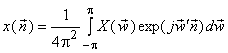 |
(3.2.1) |
Since
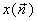 is obtained from is obtained from 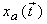 by sampling, we have: by sampling, we have:
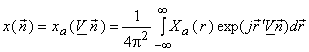
(continued in the next slide) |