The support of the ideal reconstruction filter in the frequency domain is illustrated in figure below:
Figure3.1.3 Reconstruction filter
The reconstruction filter given by equation(3.1.12) is sometimes referred to as the "ideal band limited image interpolation filter", since the reconstructed image would be identical to the original continuous image, that is ,
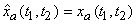provided that the original continuous image was band limited, and
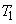and
were chosen according to Nyquist criterion;
The ideal band limited interpolation filtering can be expressed in the spatial domain by taking the inverse Fourier transform of both sides of equ (3.1.12),
Substituting the definition of
into this expression and rearranging the terms we obtain,
where
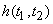denotes the impulse response of the ideal interpolation filter. For the case of rectangular sampling this is given by,
equ(3.1.2), (3.1.12), and (3.1.13) taken together form the basis of the 2D sampling theorem. It states that a band limited continuous signal may be reconstructed from its sample values. The sampling periods T1 and T2 must be small enough or equivalently the sampling frequencies
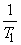and
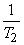must be large enough to ensure that condition of band limitedness is met.
A continuous signal that is not band limited may still be sampled, of course, but in this case equ(3.1.12) will not be true since contributions from other replicas of
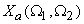in the periodic extension will fold into the region
,
.
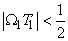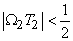This condition is called "aliasing" since high frequency components of
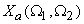will masquerade as low frequency components in
.
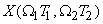can be reconstructed from its samples taken on a 2D rectangular grid by ideal low-pass filtering as follows 
for
and
