Importance of phase and magnitude
The definition indicates that the Fourier transform of an image can be complex. This is illustrated below in Figure (1. 4a-c).
  
Figure (1.4a) |
Figure( 1.4b) |
Figure( 1.4c ) |
Figure (1.4a) shows the original image  , Figure (1.4b) the magnitude in a scaled form as , Figure (1.4b) the magnitude in a scaled form as  and Figure (1.4c) the phase and Figure (1.4c) the phase 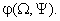 . . Both the magnitude and the phase functions are necessary for the complete reconstruction of an image from its Fourier transform. Figure(1. 5a) shows what happens when Figure (1.4a) is restored solely on the basis of the magnitude information and Figure (1.5b) shows what happens when Figure (1.4a) is restored solely on the basis of the phase information.
 
Figure(1.5a) |
Figure (1.5b) |
Figure (1.5a) figure(1.5b) shows 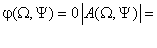 constant constant
Neither the magnitude information nor the phase information is sufficient to restore the image. The magnitude-only image Figure (1.5a) is unrecognizable and has severe dynamic range problems. The phase-only image Figure (1.5b) is barely recognizable, that is, severely degraded in quality.
Circularly symmetric signals
An arbitrary 2D signal
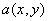 can always be written in a polar coordinate system as can always be written in a polar coordinate system as  .When the 2D signal exhibits a circular symmetry this means that: .When the 2D signal exhibits a circular symmetry this means that:
where 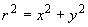 and and 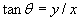 . As a number of physical systems such as lenses exhibit
circular symmetry, it is useful to be able to compute an appropriate Fourier
representation. . As a number of physical systems such as lenses exhibit
circular symmetry, it is useful to be able to compute an appropriate Fourier
representation.
The Fourier transform 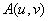 can be written in polar coordinates can be written in polar coordinates 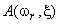 and then, for a circularly symmetric signal, rewritten as a Hankel transform: and then, for a circularly symmetric signal, rewritten as a Hankel transform:
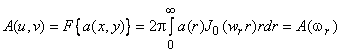 |
(1.2) |
where 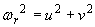 and and  is a Bessel function of the first kind of order zero. is a Bessel function of the first kind of order zero.
The inverse Hankel transform is given by:
The Fourier transform of a circularly symmetric 2D signal is a function of only the radial frequency
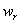 .The dependence on the angular frequency .The dependence on the angular frequency 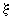 has vanished. Further if has vanished. Further if 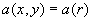 is real, then it is automatically even due to the circular symmetry. According to equ (1.2), is real, then it is automatically even due to the circular symmetry. According to equ (1.2),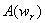 will then be real and even. will then be real and even.
|