(contd.)
The energy, E, in a signal can be measured either in the spatial domain or the frequency domain. For a signal with finite energy:
Parseval's theorem (2D continuous space) is
Parseval's theorem (2D discrete space):
This "signal energy' is not to be confused with the physical energy in the phenomenon that produced the signal. If, for example, the value a[m,n] represents a photon count, then the physical energy is proportional to the amplitude 'a', and not the square of the amplitude. This is generally the case in video imaging.
*Given three, two dimensional signals a, b, and c and their Fourier transform A, B, and C:
and
In words,convolution in the spatial domain is equivalent to multiplication in the Fourier (frequency) domain and vice-versa. This is a central result which provide not only a methodology for the implementation of a convolution but also insight into how two signals interact with each other-under convolution - to produce a third signal. We shall make extensive use of this result later.
* If a two-dimensional signal 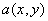 is scaled in its spatial coordinates then: is scaled in its spatial coordinates then:
* If a two-dimensional signal 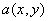 has Fourier spectrum has Fourier spectrum 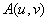 then: then:
·
If a two-dimensional signal 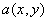 has Fourier spectrum has Fourier spectrum 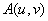 then: then:
|