From Gauss's theorem it follows that

= 0 .......................(2.51)

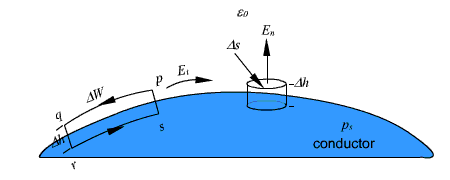
The surface charge distribution on a conductor depends on the shape of the conductor. The charges on the surface of the conductor will not be in equilibrium if there is a tangential component of the electric field is present, which would produce movement of the charges. Hence under static field conditions, tangential component of the electric field on the conductor surface is zero. The electric field on the surface of the conductor is normal everywhere to the surface . Since the tangential component of electric field is zero, the conductor surface is an equipotential surface. As = 0 inside the conductor, the conductor as a whole has the same potential. We may further note that charges require a finite time to redistribute in a conductor. However, this time is very small sec for good conductor like copper.