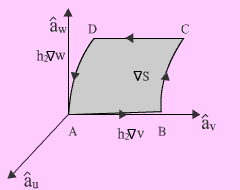
Curl of a vector field is a measure of the vector field's tendency to rotate about a point. Curl , also written as is defined as a vector whose magnitude is maximum of the net circulation per unit area when the area tends to zero and its direction is the normal direction to the area when the area is oriented in such a way so as to make the circulation maximum.

Therefore, we can write:

......................................(1.68)

To derive the expression for curl in generalized curvilinear coordinate system, we first compute and to do so let us consider the figure 1.20 :