Proof:

Let us consider a volume V enclosed by a surface S . Let us subdivide the volume in large number of cells. Let the k^th cell has a volume and the corresponding surface is denoted by S_k. Interior to the volume, cells have common surfaces. Outward flux through these common surfaces from one cell becomes the inward flux for the neighboring cells. Therefore when the total flux from these cells are considered, we actually get the net outward flux through the surface surrounding the volume. Hence we can write:

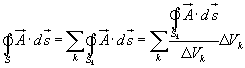......................................(1.67)

In the limit, that is when and the right hand of the expression can be written as .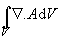

Hence we get , which is the divergence theorem.

Curl of a vector field:
We have defined the circulation of a vector field A around a closed path as .