| |
Cutt-off Frequecy of TE and TM mode |
|
For both 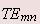 and and 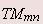 modes the phase constant is given by modes the phase constant is given by |
| |
|
|
| |
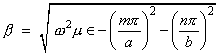 |
--------- (6.64 ) |
|
|
|
For the mode to be travelling 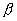 has to be a real quantity. If has to be a real quantity. If 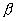 becomes imaginary then the fields no more remain travelling but become exponentially decaying becomes imaginary then the fields no more remain travelling but become exponentially decaying |
|
|
|
The frequency at which 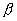 changes from real to imaginary is called the cut-off frequency of the mode. At cut-off frequency therefore changes from real to imaginary is called the cut-off frequency of the mode. At cut-off frequency therefore 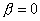 giving giving |
| |
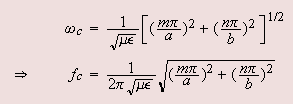 |
|
| --------- (6.65 ) |
| |
| |
| --------- (6.66 ) |
| |
|
|
|
The cut-off frequencies for lowest TM and TE modes i.e 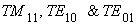 can be obtained from eqn. 6.70 as can be obtained from eqn. 6.70 as |
| |
|
|
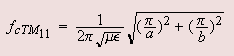 |
--------- (6.67 ) |
|
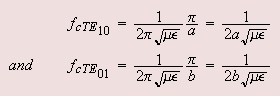 |
|
| --------- (6.68 ) |
| |
| |
| --------- (6.69) |
| |
|
|
|
Since by definition we have 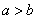 we get the frequencies as we get the frequencies as |
|
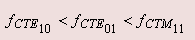 |
--------- (6.70) |
|
|
|
We can make an important observation that if at all the electro magnetic energy travels on a rectangular waveguide its |
|
frequency has to be more than the lowest cut-off frequency i.e 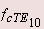 . . |
|
|
|
As the order of the mode increases the cut-off frequency also increases i.e with increasing frequency there is possibilty |
|
of existence of higher order mode. |
| |
|
|
The very first mode that propagates on the rectangular waveguide is 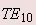 mode and therefore this mode is called the mode and therefore this mode is called the |
|
dominant mode of the rectangular waveguide. The cut-off frequency for the dominant mode is |
|
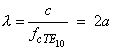 |
--------- (6.71) |
|
The equation suggest that for propagation of an electro magnetic wave inside a rectangular waveguide the width of a |
| |
waveguide should be greater than half the wave length of the wave. |
|