(a) Causal system implies that the impulse response is zero for

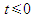
  When we take the derivative, strictly speaking we are not doing a point-wise operation, but are involving h(t-Δt)     also. However, the derivative is still zero for any given time t₀<0. so, the system remains causal.

  Stable system requires the impulse response to be absolutely integrable, i.e.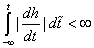

  We cannot generalise anything about this without sufficient information about h(t). For example, if h (t) = e^-tu(t) then the impulse response of the new function shows that it is stable. But if h (t) = sin (t²) then dh/dt is 2t cos(t²) which is not absolutely integrable, and the system is thus unstable.

 (b)
  Since h (t) = 0 for t<0, the given integral can be written as 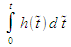  for t>0, and the integral is easily seen to  be zero for t<0. Hence the system is necessarily causal.

  For stability, we can consider a system with impulse response h(t) = e^-tu(t) so that the integral gives the response of the new system as 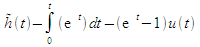which is bounded above by e^-t u (t) and hence is absolutely  integrable thus giving a stable system.
  On the other hand, we see that systems with impulse responses like    h (t) = 1/t² will not lead to a stable  derived system.