|
Solution
9 : (a)
x(t) --------LTI
system---------> y(t)
=> x(t+h) -----------------> y(t+h)
.........(1) [ from shift invariance
property]
& -x(t) -------------------> -y(t)
...........(2) [ from homogeneity]
now applying additivity in above 2 equations
x(t+h) - x(t)
--------------------> y(t+h) - y(t) ..........(3)
now applying homogeneity in equation (3)
(1/h) [ x(t+h) - x(t) ] -----------------> (1/h) [
y(t+h) - y(t) ]
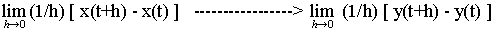
x'(t) -------------------> y'(t)
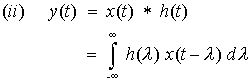
Differentiating both sides w. r. t.
t
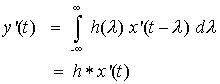
which is the output to the input x(t)
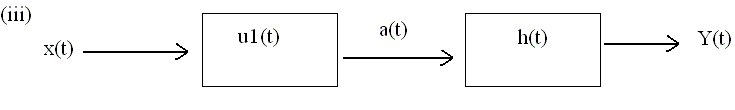 ........(1) ........(1)
Let
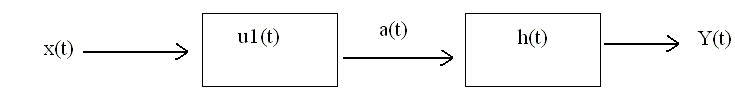
Hence a(t) = x'(t)
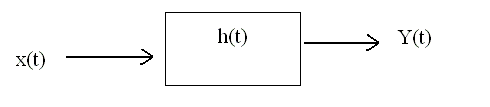
We can also write (1) as
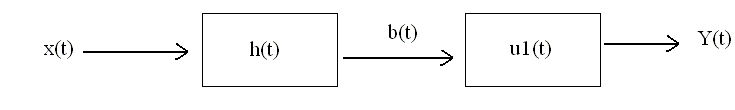
[ As Convolution is Commutative ]
=> y(t) = b(t)
=> Y(t) = y'(t)
hence output to the input x'(t) is y'(t)
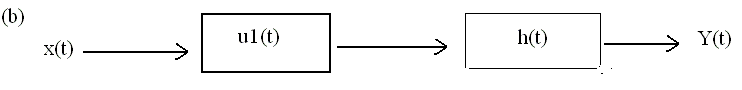
or equivalently
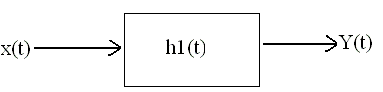
where
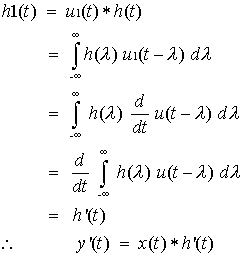
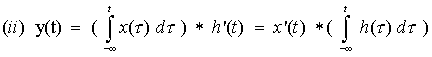
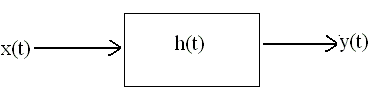
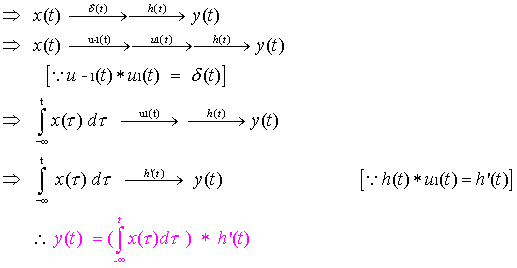
Again
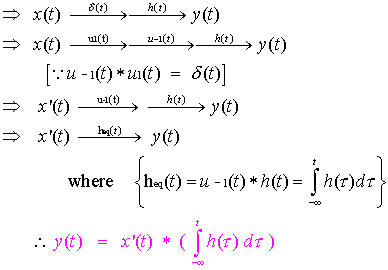
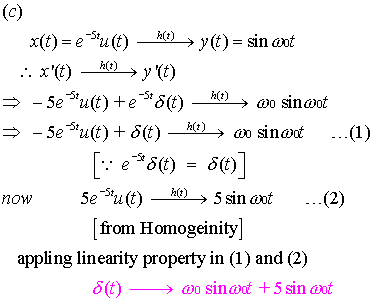
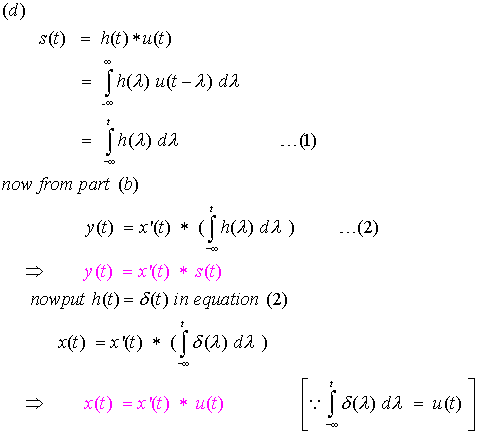
 |