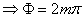
Simplifying equations we get a condition for sustained propagation of light rays inside the core as
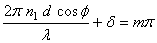
It can be noted that for 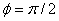 (i.e. the ray along the axis of the fiber), (i.e. the ray along the axis of the fiber), 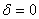 and the condition is satisfied with and the condition is satisfied with 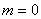 for any value of for any value of 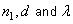 . .
As 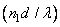 increases (either due to increase of the diameter of the core or refractive index of the core, or decrease in wavelength) more values of increases (either due to increase of the diameter of the core or refractive index of the core, or decrease in wavelength) more values of 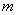 satisfy the condition and therefore have sustained propagation inside the fiber. satisfy the condition and therefore have sustained propagation inside the fiber.
The above phase condition can be satisfied only by discrete rays entering the structure i.e. rays at finite number of angles are accepted by the optical fiber. The ensemble of rays entering at a specific angle from the axis of the fiber gives discrete optical intensity distributions. These are called the modes of an optical fiber.
From the expression of the phase matching condition we find that as d increases, the number of rays accepted by the optical fiber increases and as d decreases the number of rays decreases.
Since the dispersion is due to presence of multiple rays (modes), if only one ray is made to propagate inside the fiber, there is no dispersion. So if we take a value of 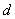 small enough such that it satisfies the phase condition only the lowest value of small enough such that it satisfies the phase condition only the lowest value of 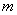 , only one mode will propagate inside the fiber. , only one mode will propagate inside the fiber. |