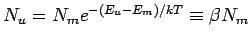
|
(4) |
where 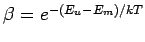 . From Eqn. (1), we have, for steady state conditions . From Eqn. (1), we have, for steady state conditions
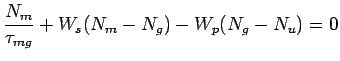
which can be simplified using Eqn. (4) to give the inversion level as
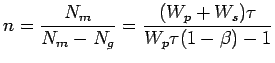
The inversion level is thus related to both the pump and signal powers and also to the pump wavelength through the Boltzmann factor.
The factor 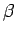 explains why 980 nm pumping is more effective in achieving population inversion than 1480 nm pumping. It was seen that because of small lifetime of the level explains why 980 nm pumping is more effective in achieving population inversion than 1480 nm pumping. It was seen that because of small lifetime of the level 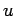 , the ions thermalize to the level , the ions thermalize to the level 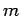 . The energy difference between these two levels is substantial ( . The energy difference between these two levels is substantial ( 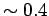 eV) as a result of which eV) as a result of which 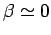 . In case of 1480 nm pumping the thermalization occurs to the lowest energy sub-level within the group . In case of 1480 nm pumping the thermalization occurs to the lowest energy sub-level within the group 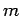 . The value of . The value of 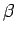 for this case is about 0.4. for this case is about 0.4.
|