Distribution functions: Consider an ideal gas of N identical particles. Let s represents the single particle state and S denotes the state of the whole system. Total energy E and the number of particles N are given by

The distribution functions can be calculated by obtaining the appropriate partition function.

MB Statistics: In this case the particles are distinguishable. The canonical partition function is given by

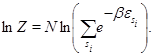
The mean number of particles in state s is then given by

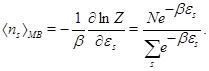
This is the Maxwell-Boltzmann (MB) distribution as already obtained classical statistical mechanics.

BE Statistics: The grand canonical partition function Z of N indistinguishable bosons is given by

The number of particles in a grand canonical ensemble is given by

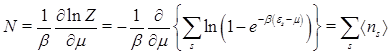
Thus the average number of molecules in the s level is

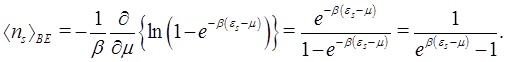
This is Bose-Einstein (BE) distribution where always , otherwise could be negative.