Example: Consider a free particle of mass m inside a one dimensional box of length L, such that , with energy between E and . The macroscopic state of the system is defined by with N=1. The microstates are specified in certain region of phase space. Since the energy of the particle is , the momentum will be and the position q is within 0 and L. However, there is a small width in energy , so the particles are confined in small strips of width as shown in Fig.1.1 ( a). Note that if , the accessible region of phase space representing the system would be one dimensional in a two dimensional phase space. In order to avoid this artifact a small width in E is considered which does not affect the final results in the thermodynamic limit. In Fig.1.1 ( b), the phase space region of a one dimensional harmonic oscillator with mass m, spring constant k and energy between E and is shown. The Hamiltonian of the particle is: and for a given energy E, the accessible region is an ellipse: . With the energy between E and , the accessible region is an elliptical shell of area .

Microstates of quantum particles: For a quantum particle, the state is characterized by the wave function . Generally, the wave function is written in terms of a complete orthonormal basis of eigenfunctions of the Hamiltonian operator of the system. Thus, the wave function may be written as

where is the eigenvalue corresponding to the state . The eigenstates , characterized by a set of quantum numbers n provides a way to count the microscopic states of the system.

Example: Consider a localized magnetic ion of spin 1/2 and magnetic moment μ in thermal equilibrium at temperature T. The particle has two eigenstates, (1,0) and (0,1) associated with spin up (↑) and down spin (↓) respectively. In the presence of an external magnetic field , the energy is given by

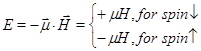
Thus, the system with macrostate (N,H,T) with N=1 has two microstates with energy and corresponding to up spin (parallel to ) and down spin (antiparallel to ). If there are two such magnetic ions in the system, it will have four microstates: with energy , with zero energy and with energy . For a system of N spins of spin- 1/2, there are total microstates and specification of the spin-states of all the N spins will give one possible microstate of the system.