| |
8.5.1 Bismuth Ferrite (BiFeO3)
One of the most studies multiferroic is Bimusth ferrite or BiFeO3 (BFO), primarily because it has very high ferroelectric transition temperature (TC = 1100 K)6 and shows G-type antiferromagnetism with cycloidal spin structure with Neel temperature (TN) of ~ 650 K.7
In its ferroelectric state, as shown in Figure 8.2, BFO possesses a rhombohedrally distorted ABO3 type perovskite structure with space group R3c having lattice parameters, ar = 3.965 Å and 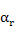 = 89.4° at room temperature.8 Above the Curie temperature, the structure changes to a high symmetry cubic phase. = 89.4° at room temperature.8 Above the Curie temperature, the structure changes to a high symmetry cubic phase.
| Figure 8.2 Schematic diagram of the crystal structure of BiFeO3 |
The material has been shown to be ferroelectric at room temperature in both single crystal and thin film form high remanent polarization, more than 50 μC/cm2. 9,10 However, polycrystalline thin films can be leaky depending upon the methods of preparation and other conditions.11 On the other hand, while magnetic character of pure phase in single crystal form is antiferromagnetic, there have been a few controversies on magnetism in thin films. Often, impurities like Fe2+ and other iron borne impurities as well as deoxygenation can result in significant magnetism.12 The material is also prone to containing defects as well as difference valencies of Fe which can alter the material properties.
The periodic spin spiral results in zero magnetic moment and hence linear magnetoelectric effects average to approximately zero. However, properties of BiFeO3 can also be altered by making chemical substitutions. For example substitution of A-site cation (Bi) by ions such as Ba or Nd13 gives rise to significant magnetism in the compound while substitution of B-site cation (Fe) by elements such as Zr14 results in alteration in the defect chemistry as well as change in the leakage characteristics of the material. These effects are attributed to the breaking of spin spiral upon doping. Similarly, epitaxial constraints can also result in this breaking of spin spirals.
| 6R. Teague, R. Gerson, and W. J. James, Solid State Commun. 8, 1073 (1970) |
| 7P. Fischer, M. Polomska, I. Sosnowska, and M. Szymanski, J. Phys. C 13, 1931 (1980) |
| 8G Catalan and J.F. Scott, Advanced Materials, 21, 2463 (2009). |
| 9D. Lebeugle, D. Colson, A. Forget, M. Viret, P. Bonville, J. F. Marucco, and S. Fusil, Phys. Rev. B 76, 024116 (2007). |
| 10J. Wang, J. B. Neaton, H. Zheng, V. Nagarajan, S. B. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D. G. Schlom, U. V. Waghmare, N. A. Spaldin, K. M. Rabe, M. Wuttig, and R. Ramesh, Science 299, 1719 (2003) |
| 11A. Z. Simoes, A. H. M. Gonzalez, L. S. Cavalcante, C. S. Riccardi, E. Longo, and J. A. Varela, J. Appl. Phys. 101, 074108 (2007). |
| 12H. Bea, M. Bibes, A. Barthelemy, K. Bouzehouane, E. Jacquet, A. Khodan, J. P. Contour, S. Fusil, F. Wyczisk, A. Forget, D. Lebeugle, D. Colson and M. Viret, Applied Physics Letters 87 (7), 072508 (2005). |
| 13V. A. Khomchenko, D. A. Kiselev, M. Kopcewicz, M. Maglione, V. V. Shvartsman, P. Borisov, W. Kleemann, A. M. L. Lopes, Y. G. Pogorelov, J. P. Araujo, R. M. Rubinger, N. A. Sobolev, J. M. Vieira, and A. L. Kholkin, J. Magn. Magn. Mater. 321, 1692 (2009). |
| 14S. Mukherjee, R. Gupta, A. Garg, V. Bansal, and S. Bhargava, J. Appl. Phys. 107, 123535 (2010) |
|