5.5.2 Theory of Piezoelectric Materials

From the fundamentals discussed in Module 4, we can write that when an electric field E is applied to a material, the total dielectric displacement i.e. charge per unit area of the plates on both side of pyroelectric material i.e. D can be expressed as

(5.37)

Here ε is permittivity of the pyroelectric material and P_s is the spontaneous polarization.

Assuming electric field, E, as constant, differentiating the above equation with temperature leads to

(5.38)

Now, defining generalized pyroelectric coefficient, Δp_g, as change in polarization with temperature, we write

Δ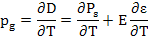

OR

Δ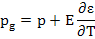

(5.39)

Here p is defined as true pyroelectric coefficient. The last term in the above equation is the temperature dependence of the permittivity of the material which we can measure.

Since polarization is a vector, the pyroelectric coefficient is also a vector and has three components as defined by

(5.40)

The above equation neglects the change in dielectric constant with temperature and is valid only when such assumption is true. However, in practice, the electrodes collecting the charges are normal to the polar axis, and we treat these quantities as scalars. The coefficient is usually negative because polarization decreases with temperature.

As you have seen in previous sections, the behavior of polarization with temperature is dependent on the nature of transition, naturally the pyroelectric coefficients are much larger in magnitude for second order transition than for first order transition and hence are more useful.