6.1 Magnetic Moments
Magnetism in materials is crudely explained as mutual attraction between two pieces of a material, say iron or iron ore. There are various microscopic mechanisms of magnetism in materials which are shown later. The strength of magnetism is quantitatively judged by a quantity called as ‘magnetic moment’. This magnetic moment should not be confused with dipole moment as we learnt in Module 4.
The major contributors of magnetic moment in a material are
Motion of electrons in an orbit of an atom. Orbital moment can be related to the current flowing in a loop of a wire of zero (negligible) resistance. -
Spinning of electron around it own spin axis gives rise to a moment.
-
Nuclear magnetic moment due to nuclei.
The first two contributions are quite significant and contribute to most of the magnetic character of a material while the third component, nuclear magnetic moment, is rather insignificant in the context of most magnetic materials of practical interest and can be neglected.
6.1.1 Orbital Moment
According to Ampere’s law, when a current flows through a coil, it gives rise to a magnetic field in a direction perpendicular to the plane of the loop. The field is related to the current by
where N is the number of loops per unit length of the coil, I is the current in Amperes and H is the induced magnetic field in Ampere per m i.e. A.m-1.
| Figure 6.1 A current carrying coil |
Now based on classical physics, the current, I, is nothing but charge per unit time and is expressed as
The time is nothing but the circumference divided by the velocity of electron, v, i.e. t = 2π r/v which can be substituted in equation (6.2) to yield
where r is the radius of the orbital.
Therefore, the orbital magnetic moment, μorbit, which is a product of current, I, and area, A = πr2 can be expressed as
or
where q is the charge of electron which equals to – e; v is velocity of electron; m is the mass of electron and J is the angular momentum which is equal to mvr..
The equation (6.4) shows that orbital moment can be expressed in the multiple of angular momentum.
6.1.2 Spin Moment
As we saw earlier, spinning of electron about its own axis also gives rise to a moment. For purely quantum mechanical reasons, for an electron spinning around its own axis, the ratio of spin magnetic moment to angular moment is twice as large as for orbital moment i.e.
6.1.3 Net Magnetic Moment
So the net magnetic moment for an atom containing several atoms is basically net sum of these two contributions.
Although it is not possibly to explain classically, from quantum mechanics, the ratio of magnetic moment to the angular momentum always works out to be between 1 and 2, related by a factor called a Landé g-factor (g) purely because net moment is the sum of these two and can be expressed as
Value of g would be 1 for purely orbital moment and 2 for purely spin moment. The latter is true for many ferrites where orbital magnetic moment is thought as quenched and the dominating contribution to magnetic moment arises from spin magnetization.
Again, quantum mechanics argues that the angular momentum can take only certain values defined by orbital and spin quantum number, I and s respectively.. Hence the angular moment for an electron with a characteristic number, j is expressed as
where 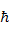 is equal to h/2π;; h being Planck’s constant (=6.6×10-34 J.s1). The characteristics number j can be orbital quantum number, l, for orbital moment and spin quantum number, s, for spin moment.
Since magnetic moment is now quantized as a result of angular momentum being quantized, for an electron, we can define a basic quantum unit of magnetic moment as Bohr magneton, μB, as
The value of one Bohr magneton is 9.274×10-24A.m2.
Nuclear magnetic moment is only of the order of 10-3 μB and hence is neglected for most cases.
| 
