4.10 Impedance Spectroscopy
The frequency response of the impedance of above circuit would also yields a semi-circle in the complex plot between real and imaginary parts of the dielectric constant and such a response represent a capacitor with losses. Such technique of characterizing dielectrics is called Impedance Spectroscopy.
The intercepts of the semi-circle on the x-axis represent high and low frequency dielectric constants or εr∞' and εrs' respectively.
The maxima of the semi-circle occurs at
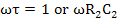 |
(4.115) |
The semicircle equation turns out to be
which can be obtained by removing ωτ from the equations (4.105a) and (4.105b).
| Figure 4.29 Cole-Cole Plot |
Alternatively in a semi-circle one can draw two vectors, X and Y which are always perpendicular to each other and are related as y = -iωτ.xThis relation can easily be obtained just by using the Debye’s equation (4.98) and simple vector additions and subtractions.
Basically any point on the surface of the semi-circle of diameter (εrs' - εr∞' ) in this complex plane can be defined by these vectors.
In the figure above, a perfect semicircle represents a narrow distribution of relaxation times indicating only one primary mechanism of polarization.
However, if there is the presence of a tail on the
low frequency side, as shown by dashed line i.e. increasing εr'' , indicates large distribution of relaxation times and usually is due to high losses in the material.
In case a material has more than one contribution to the impedance, which is often the case with polycrystalline ceramics where grain, grain boundaries and electrode-ceramic interface have distinct contributions, then one can witness more than one semi-circle, often overlapping each other. An idealized picture of such a scenario can be see below. One of the ways to model such a behavior may be using three series-parallel RC elements circuit as shown below.
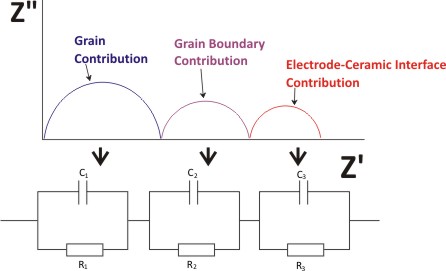 |
| Figure 4.30 Cole-Cole Plot and possible equivalent circuit for a solid with multiple polarization mechanisms |
|