4.7.1 Description of Ionic and Electronic Phenomenon
If we assume charge dipoles behaving like a linear harmonic oscillator, then they also follow the its equation of motion.
The equation of motion describing an oscillating system driven by a sinusoidal force can be written as
 |
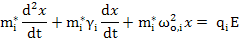(4.77) |
where mi* is the mass of the particle (i.e. charges or ions containing charges), i, x is the displacement from the equilibrium, γi is the friction coefficient on the species and ω0,i is the natural frequency of the particle. In this equation, on the left hand side, the first term is the force due to acceleration, the second term is the damping or frictional force, and the third term is the spring restoring force, while the term on the right hand side is the force due to applied electric field.
The field will actually be local field than just the applied field but for the sake of simplicity, we can assume the system to behave like a gas consisting of N atoms per unit volume for which qi = -Zie.
Consider two cases:
Case I: When the applied field in d.c. and is switched off at a given moment
Restoring force pulls back the charges to equilibrium. If friction is zero, there will be no damping of oscillations. If friction is present, then system will have damped oscillations.
Case II : When applied field is sinusoidally varying field i.e.
 |
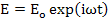(4.78) |
The corresponding displacement is given as
 |
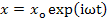(4.79) |
Ignoring transient terms, the solution of equation (4.78) is
 |
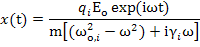(4.80) |
The induced dipole moment per particle is
 |
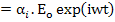(4.82) |
where αiis the electronic or ionic polarizability as be the case. If the friction term is neglected, then frequency dependent polarizability is
 |
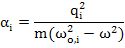(4.83) |
Here mass, mi, is either the mass of electrons in atoms or ions in crystals.
In case of ionic polarization, one takes the reduced mass which is given as {M+ M- / (M++ M-)} where M+ and M- are cation and anion masses respectively. Similarly qi will be charge on the particle as appropriate and ω0,i will be natural frequency of electronic or ionic polarization mechanisms.
The polarization can then be written as
 |
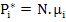(4.84) |
Hence using equations (4.15) and (4.16) we get the expressions for the susceptibility and dielectric constant as
 |
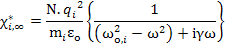(4.85) |
and
 |
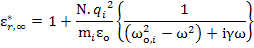(4.86) |
Here * implies that these are complex quantities which was also mentioned earlier when we discussed power dissipation characteristics in real dielectrics.
The subscript ∞ signifies the susceptibility and dielectric constants at frequencies below the resonance frequencies. Resonance for electronic polarization occurs at about 1015 s-1 and for ionic polarization occurs at about 1013 s-1.
Now, we can separate out the real and imaginary parts of the dielectric constants as following
 |
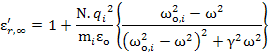(4.87) |
and
 |
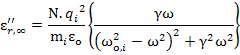(4.88) |
These can be plotted vs frequency as shown below.
| Figure 4.20 Schematic plot of real and imaginary parts of dielectric constant for electronic and ionic polarization |
The value of resonance frequency can be determined from the polarizability expressions we determined above in equations (4.34) and (4.39) as we know that 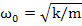 . All now you need to do is to balance the force inducing the moment and the restoring force to find out the spring constant. The value of ω0 works out to be about 1013 Hz for ionic and 1015 Hz for electronic polarization mechanism. This makes sense because for ionic polarization, the masses of ions are several thousand times higher than electrons and 1013 Hz is very close to the natural frequency of lattice vibrations!
The shape of the plot should also help you understand the far right portion of the dielectric constant versus frequency plot shown earlier when we discussed mechanisms of polarization. For very frequencies when ω → ∞, εr' = 1 or ε' = ε0.
You must remember that the above discussion is valid for gases with non-interacting dipoles for we assumed that local field was equal to the applied field. If we use the local field instead of the applied field i.e. Eloc= E/3(εr'' + 2), fortunately we don’t change the form of expressions, rather we get only a shift in the resonance frequency. The changed resonance frequency is  .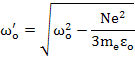
Naturally for a system with ionic polarization, electronic polarization will be in-built simply because anything is made of atoms. |
