| |
4.5.2 Ionic Polarization
The figure below shows that in an ionic solid, in the absence of an external electric field, all the dipoles (formed by each Na+ and Cl- pair with an equilibrium separation distance as do cancel each other due to crystal symmetry and hence net dipole moment is equal to zero. Remember, in these solids, no dipole rotation is allowed.
However, when a finite field, E, is applied, the force experienced by the ions leads them to move away from their equilibrium positions , as shown in the figure, giving rise to unequal dipole moments in different directions and as a result, the material will have net dipole moment.
| Figure 4.11 Schematic of the ionic polarization |
As you can now see, the distance between the ions decreases by ‘d’ in one direction and increases by ‘d’ in the opposite direction.
Now we calculate the magnitude of ‘d’.
The force, F1, which increases the distance between the ions of charge, q, can be expressed as
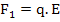 |
(4.35) |
However, there is a force, F2, in the other direction trying to restore the equilibrium between the ions which is expressed as
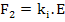 |
(4.36) |
Where ki can be considered as spring constant of the bond between ions assuming ionic dipoles behave like springs.
The spring constant can be expressed in terms of elastic modulus, Y, and can be expressed as
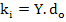 |
(4.37) |
At equilibrium, F1 = F2 and by combining equations (4.35-4.37), we get an estimate of d i.e.
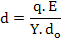 |
(4.38) |
Hence, induced ‘extra’ dipole moment, μ, will be
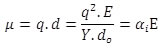 |
(4.39) |
where αi is ionic polarizability. Thus the polarization, P, can be written as
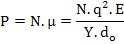 |
(4.40) |
where N is the dipole density per unit volume.
Note: Here we considered the electric field, E, parallel to the main crystallographic axis. If this is not the case, one needs to take the component of dipole moment in the direction of the field before adding them together.
This is a very a rough guide to the calculation of the ionic polarization and can be more complex in the case of many ionic solids, especially when ions do not have similar charges. For example, in calcium fluoride, CaF2, a material used for making lenses for lithography machine, the dielectric constant is approximately equal to n2. This enables the lenses to be made of dimensions of about 0.1 mm.
The above expressions also tell us that stronger bonds lead to smaller polarization which seems obvious because then you wouldn’t be able to stretch the atoms too far!
The following are the values of the dielectric constant of some materials where ionic polarization contributes (in addition to electronic polarization of course) (source : “Solid State Physics” by N.W. Ashcroft and N.D. Mermin):
| ZnO |
4.6 |
| ZnS |
5.1 |
| ZnSe |
5.8 |
| CdSe |
7.0 |
| MgO |
3.0 |
| CdS |
5.2 |
| BeO |
3.0 |
|