4.5 Analytical Treatment of Polarizability
Here we discuss the simple analytical solutions for determining the polarizability and polarization for each of the above polarization mechanisms. The analysis will shed some light on the dependence of polarizability on the material parameters as well as any external parameters.
4.5.1 Electronic Polarization
To achieve this, let us first imagine an atom as a perfect sphere, having +Ze charge at the center of the nucleus and an equivalent –Ze charge of electrons around it. Here R is the radius of the atom.
| Figure 4.10 Schematic of electronic polarization |
Under the application of a electric field, E, the force F1, on the charges is given as
As a result, positive and negatives charges experience forces in different direction and their center move away from each other by a distance, d.
However, d has to be finite values because this force is balanced by Coulomb force of attraction between opposite charges which can be calculated by simple electrostatistics and is given as
Equating the two forces, gives the equilibrium separation distance do, i.e.
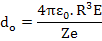 |
(4.31) |
Induced dipole moment, μ, would be
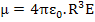 |
(4.32) |
If dipole density was N, the polarization is given as
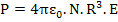 |
(4.33) |
Using equation (4.15), we can get electronic susceptibility, χe, and electronic polarizability, αe, as
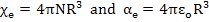 |
(4.34) |
This is a very important result as it allows us to work out the electronic contribution to the dielectric constant. This also shows the linear relationship between polarization and electric field for electronic polarization mechanism. Another point to note is that polarizability of atoms with s- and p- atoms i.e. alkali and rate-earth is more than that of transition elements i.e. d-atoms due to higher shielding of nucleus by electrons in d-atoms.
The equation (4.34) also shows that the larger the atom, the larger is the polarization! Moreover, anions are more polarizable than cations as electrons in anions' outer shells are more loosely bound.
The values for atomic polarizability of some atoms are given below:
F |
1.2 |
Li |
0.03 |
Cl |
3 |
Na |
0.3 |
Br |
4.5 |
K |
0.9 |
I |
7 |
Rb |
1.7 |
4.5.1.1 Examples
Assume a typical value for dipole density, N, and atomic radius, R, for a material made up of atoms with spherical symmetry of orbitals, i.e. N=4*1019 cm and R ≈ 7*10-9 cm, yielding
which is a very small value and the relative dielectric constant,εr, does not increase by much.
What it says is that the electronic polarization effect is generally very weak and contributes very little to the overall polarization. Having said that, it must be borne in mind that some materials like Si which are covalently bonded and orbital do not have spherical symmetry and as a result the dielectric constants can be higher (for example Si has about εr ~ 12). For electronic polarization, εr is also equal to n2 and hence, if one knows the refractive index, this works as a check for the values calculated.
Values for some materials where electronic polarization is the principle mechanism of polarization are given below (source: "Solid State Physics” by N.W. Ashcroft and N.D. Mermin):
| Carbon (diamond) |
5.7 |
| Ge |
16.0 |
| GaP |
8.4 |
| Si |
12.0 |
| SiC |
6.7 |
| GaAs |
10.9 |
|