4.1.4 Polarization Charges
In a parallel plate capacitor without any dielectric, the surface charge in vacuum σs is
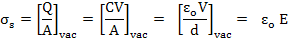 |
(4.10) |
where E is the applied field due to the potential V between the plates.
In the presence of a dielectric, the net charge density now becomes
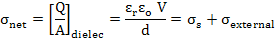 |
(4.11) |
σexternal is nothing but to due to presence of dielectric and due to polarization of charges and can be written as σpol. Hence,
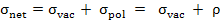 |
(4.12) |
where ρ is the extra charge resulting from the polarization of the dielectric.
According to the electromagnetic theory, the surface charges on the plates can be defined as dielectric displacement, D, such as
OR
OR
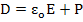 |
(4.13) |
The equation shows that the total charge on the plates of a capacitor with dielectric inserted between the plates is now the sum of the surface charge present in a vacuum capacitor (ε0.E) and extra charge resulting from polarization of the dielectric material, ρ.
Hence, we can now write dielectric displacement as,
 |
(4.14) |
OR
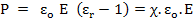 |
(4.15) |
where 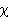 is called dielectric susceptibility and is expressed as is called dielectric susceptibility and is expressed as
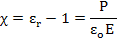 |
(4.16) |
This implies that susceptibility is nothing but the ratio of polarized charge or excess charge to the surface charge in a vacuum capacitor.
Now the question arises: What is the reason for polarization? It can be said that it is basically due to short range movement of masses i.e. electrons, or atoms or molecules under applied electric field. Such a movement is not likely to occur arbitrarily fast, rather it is a function of the frequency of the applied field. This also implies that the dielectric properties are also a function of the frequency. These properties are also a function of material structure and temperature. But for now, we will turn our attention to the understanding of basics of mechanisms of polarization and qualitatively what it means in terms of applied frequency. |