4.1.2 Polarization and Surface Charge
| Figure 4.2 Schematic of a dielectric between two plates |
Imagine a parallel plate capacitor with homogeneously distributed polarized material between the plates.
Assume that all the dipole moments are aligned in the same direction. Now, if we look at the charge density in a small volume of the material (circle inside the capacitor), then it is clearly zero since both positive and negative charges are equal.
While at the surface, there is a finite charge as shown by the small circle. On both surfaces, the charges move out by a tiny distance, dx, which is nothing but surface polarization charge which can be calculated.
The number of charges, nc, on the surface area A is equal to the number of dipoles contained within a surface volume (V=A.dx) times the charge of the dipole, q which is nothing but equivalent to one layer of the surface charge.
Assuming homogeneous distribution of the dipoles, polarization can be written as
where the subscript ‘s’ implies the surface. Hence
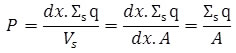 |
(4.3) |
where ∑s implies sum over the surface volume. Hence
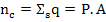 |
(4.4) |
So the surface charge density σ
is
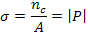 |
(4.5) |
σ is a scalar quantity if P.A is scalar.
If polarization is not normal to the surface then
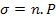 |
(4.6) |
where n is the outward pointing unit vector normal to the surface of the polarized material. |