2.18.1 For a Pure or Intrinsic Compound (semiconductor or insulator)
Concentrations of electrons (ne) and holes ((nh) are equal at any temperature and are given as
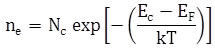 |
(2.71) |
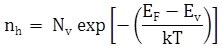 |
(2.72) |
where Nc and Nv are defined as effective conduction and valence band density of states and are expressed as
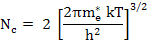 and and 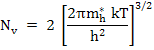 |
(2.73) |
Here me* and mh* are the effective mass of electron and holes respectively, k is the Boltzmann’s constant, h is the Planck’s constant and T is the temperature. The value of Nc and Nv is ~1019 cm-3 at 300 K.
Electron and hole concentrations in the conduction and valence bands are equal i.e.
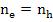 |
(2.74) |
Fermi energy is defined as
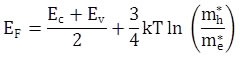 |
(2.75) |
where 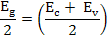 . .
In oxides, me* and mh* are generally 2-10 times larger than the mass of free electron, me. Since, the atomic density of solids is about 1023 cm-3, the density of states is about four order of magnitude lower than that in semiconductors.
Moreover, if the second term in equation (2.75) is small and is actually zero if me* = mh* , then Fermi level is quite close to the center of the band gap.
Hence for an intrinsic compound where ne = nh.
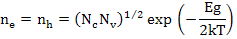 |
(2.76) |
Fermi level usually remains in the middle of the band gap but can shift up or down when materials is doped. Typically EF moves up, from the center of the bandgap towards EC , for n-type doping and moves down for p-type doping.
The above expressions have striking similarity to the concentration of lattice defects where
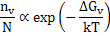 |
(2.77) |
The density of electronic states may be thought of as equivalent to the density of vacancies in the lattice sites.
The excitation of electrons across the band gap can be depicted by a chemical defect reaction as follows
The equilibrium constant is
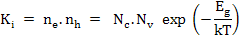 |
(2.78) |
At 300K
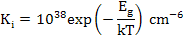 |
(2.79) |
Here Ki is not unit-less unlike the reaction constant in the defect reactions because ne and nh have the units of cm-3.
|