- A control mass or closed system is characterized by a fixed quantity
of mass of a given identity, while in an open system or control volume
mass may change continuously due to the flow of mass across the system
boundary.
- Continuity equation is the equation of conservation of mass in a fluid flow. The general form of the continuity equation for an unsteady
compressible flow is given by
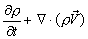 where, where, 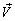 is the velocity vector is the velocity vector |
|
- The concept of stream function is a consequence of continuity. In a
two dimensional incompressible flow, the difference in stream functions
between two points gives the volume flow rate (per unit width in a
direction perpendicular to the plane of flow) across any line joining the
points. The value of stream function is constant along a streamline.
- The equation of motion (conservation of momentum) of an inviscid flow
is known as Euler’s equation. The general form of Euler’s equation is given by
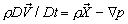 , where , where 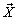 is the body force vector
per unit mass and is the body force vector
per unit mass and 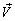 is the velocity vector. Euler’s equation along a
streamline, with gravity as the only body force, can be written as is the velocity vector. Euler’s equation along a
streamline, with gravity as the only body force, can be written as
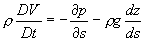 ( where s represents the coordinate along the streamline.) ( where s represents the coordinate along the streamline.)
- Reynolds transport theorem states the relation between equations applied
to a system and those applied to a control volume. The statement
of the law of conservation of momentum as applied to a control volume
is known as momentum theorem. This theorem states that the resultant
force (or torque) acting on a control volume is equal to the time
rate of increase in linear momentum (or angular momentum) within
the control volume plus the rate of net efflux of linear momentum (or
angular momentum) from the control volume.
- A fluid element in motion possesses intermolecular energy, kinetic energy
and potential energy. The work required by a fluid element to
move against pressure is known as flow work. It is loosely termed as
pressure energy. The shaft work is the work interaction between the
control volume and the surrounding that takes place by the action of
shear force such as the torque exerted on a rotating shaft. The equation
for conservation of energy of a steady, in viscid and incompressible flow in a conservative body force field is known as Bernoulli’s equation.
Bernoulli’s equation in the case of gravity as the only body force field
is given by
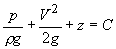 (The value of C remains constant along a streamline.) (The value of C remains constant along a streamline.)
- The loss of mechanical energy due to friction in a real fluid is considered
in Bernoulli’s equation as
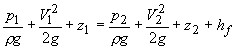
where, hf = frictional work done or loss of mechanical energy due to friction per unit weight of a fluid element while movingfrom station 1 to 2 along a streamline. The term hf is usually referred to as head loss. |