|
Exercise Problems - Chapter 4
1. Which of the following velocity fields are kinematically possible for an incompressible flow ?
(i) u = x2 + y2 , v = y2 + z2 , w = -2 (x + y) z
(ii) 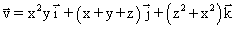
(iii) 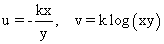
(iv) 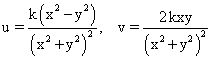
(k is a constant) [(i) yes, (ii) No, (iii) yes, (iv) No]
2. The x component of velocity in a two-dimensional incompressible flow is prescribed as u = By3 - Ax4 , where A and B are constants. Find out the y component of velocity. Assume that for all values of x, v = 0 at y = 0. Check whether the flow is irrotational.
[ v = 4 Ax3y, No ]
3. Consider a vertical nozzle of inlet and outlet diameters of 0.6 m and 0.3 m respectively as shown in Fig 13.2. The pressure at section 1 is 20 kPa (gauge), and the volume flow rate is 0. 6 m3 /s. Find
(i) the velocities at section 1 and section 2,
(ii) total force acting on the walls of the nozzle.
[Neglect frictional resistance]
[(i) V1 = 2.12 m/s, V2 = 8.45 m/s
(ii) 0.517 kN (vertically upwards]
|
Fig 13.2
4. Water flows through a 5 m high conical vertical pipe whose diameter changes from 0.5m at the top end to 1.5 m at the bottom end. Measurements indicate that when velocity at the smaller section is 18 m/s, the frictional head loss is 1m of water for flow in either direction. For a pressure of 1.8 m of water gauge at the smaller section, determine the pressure ( in meter of water gauge) at the larger section when the flow is (i) in the downward direction, (ii) in the upward direction.
[ (i) 24. 11m, (ii) 26.11 m]
5. A force of 1 kN is required to hold the plate in position for a flow of oil of specific gravity of 0. 8 as shown in Fig.13.3. Find the velocity V of the flow of oil
[42 m/s]
Fig 13.3
6. Water flows as two free jets from the tee attached to the pipe shown in Figure 13.4 below. The exit speed is 15 m/s. If viscous effects and gravity are negligible, determine the x and y components of the force that the pipe exerts on the tee.
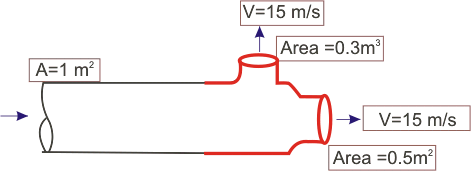
Fig 13.4
7. A horizontal jet of water with velocity V and cross sectional area A impinges on a stationary vane, which deflects the jet through an angle θ (see Fig 13.5). Derive expressions for the horizontal and vertical force components X and Y acting on the vane. Neglect effects of gravity and friction.
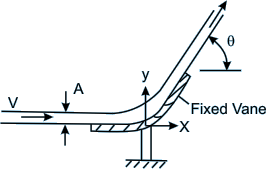
Fig 13.5
To
view the recap, click next button or select from left-hand-side. |
|