Exercise Problems  -  Chapter 1

1. A thin film of liquid flows down an inclined channel. The velocity distribution in the flow is given by

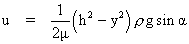
where, h = depth of flow, α = angle of inclination of the channel to the horizontal, u = velocity at a depth h below the free surface, ρ = density of liquid, μ = dynamic viscosity of the fluid. Calculate the shear stress: (a) at the bottom of the channel (b) at mid-depth and (c) at the free surface. The coordinate y is measured from the free surface along its normal

[(a) α,   (b) α ,   (c) 0]

2. Two discs of 250 mm diameter are placed 1.5 mm apart and the gap is filled with an oil. A power of 500 W is required to rotate the upper disc at 500 rpm while keeping the lower one stationary. Determine the viscosity of the oil.

3. Eight kilometers below the surface of the ocean the pressure is 100 MPa. Determine the specific weight of sea water at this depth if the specific weight at the surface is 10 kN/m³ and the average bulk modulus of elasticity of water is 2.30 GPa. Neglect the variation of g.

4. The space between two large flat and parallel walls 20 mm apart is filled with a liquid of absolute viscosity 0.8 Pas. Within this space a thin flat plate 200 mm × 200mm is towed at a velocity of 200 mm/s at a distance of 5 mm from one wall. The plate and its movement are parallel to the walls. Assuming a linear velocity distribution between the plate and the walls, determine the force exerted by the liquid on the plate.

5.  What is the approximate capillary rise of water in contact with air (surface tension 0.073 N/m) in a clean glass tube of 5mm in diameter?