|
Rotation
Figure 8.3 represent the situation of
rotation
Observations from the figure:
-
The transverse displacement
of B with respect to A and the lateral displacement of D with
respect to A (Fig. 8.3) can be considered as the rotations
of the linear segments AB and AD about A.
- This brings the concept
of rotation in a flow field.
Definition of rotation at a point:
The rotation at a point is defined
as the arithmetic mean of the angular velocities
of two perpendicular
linear segments meeting at that point.
Example: The angular velocities
of AB and AD about A are
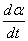 and and
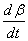 respectively. respectively.
Considering the anticlockwise direction as positive, the rotation at A can be written as,
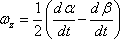 |
(8.5a) |
or
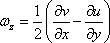 |
(8.5b) |
The suffix z in
ω represents the rotation about z-axis.
When
u = u (x, y)
and
v = v (x, y) the
rotation and angular deformation of a fluid element exist simultaneously.
Special case :
Situation of pure Rotation
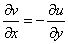 , ,
 and and 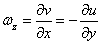
Observation:
- The linear segments AB and AD move with the same angular velocity (both in magnitude and direction).
- The included angle between them remains the same and no angular deformation takes place. This situation is known as
pure rotation.
|