Translation with Linear Deformations

         Observations from the figure:

       Since u is not a function of y and v is not a function of x

• All points on the linear element AD move with same velocity in the x direction.
  
  
• All points on the linear element AB move with the same velocity in y direction.
  
  
• Hence the sides move parallel from their initial position without changing the included angle.

       This situation is referred to as translation with linear deformation.

       Strain rate:

The changes in lengths along the coordinate axes per unit time per unit original lengths are defined as the components of linear deformation or strain rate in the respective directions.

       Therefore, linear strain rate component in the x direction

and, linear strain rate component in y direction

Rate of Deformation in the Fluid Element

         Let us consider both the velocity component u and v are functions of x and y, i.e.,

Figure 8.3 represent the above condition

        Observations from the figure:

• Point B has a relative displacement in y direction with respect to the point A.
  
• Point D has a relative displacement in x direction with respect to point A.
  
• The included angle between AB and AD changes.
  
• The fluid element suffers a continuous angular deformation along with the linear deformations in course of its motion.

          Rate of Angular deformation:

The rate of angular deformation is defined as the rate of change of angle between the linear segments AB and AD which were initially perpendicular to each other.

Fig 8.3   Fluid element in translation with simultaneous linear and angular deformation rates

           From the above figure rate of angular deformation,

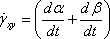(8.1)

From the geometry

	(8.2a)
	(8.2b)

Hence,

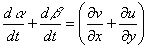(8.3)

Finally

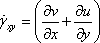(8.4)