Streamlines

      Definition: Streamlines are the Geometrical representation of the of the flow velocity.  

      Description:

•  In the Eulerian method, the velocity vector is defined as a function of time and space coordinates.

•  If for a fixed instant of time, a space curve is drawn so that it is tangent everywhere to the velocity vector, then this curve is called a Streamline.
   

          Therefore, the Eulerian method gives a series of instantaneous streamlines of the state of motion (Fig. 7.2a).

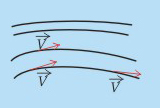
Fig 7.2a    Streamlines

       Alternative Definition:

A streamline at any instant can be defined as an imaginary curve or line in the flow field so that the tangent to the curve at any point represents the direction of the instantaneous velocity at that point.

       Comments:

• In an unsteady flow where the velocity vector changes with time, the pattern of streamlines also changes from instant to instant.

• In a steady flow, the orientation or the pattern of streamlines will be fixed.

From the above definition of streamline, it can be written as

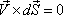(7.3)

        Description of the terms:

        1. 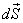is the length of an infinitesimal line segment along a streamline at a point .

        2. 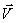 is the instantaneous velocity vector.

The above expression therefore represents the differential equation of a streamline. In a cartesian coordinate-system, representing

the above equation ( Equation 7.3 ) may be simplified as

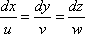(7.4)

Stream tube:

A bundle of neighboring streamlines may be imagined to form a passage through which the fluid flows. This passage is known as a stream-tube.

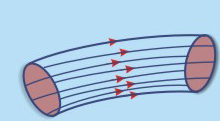
Fig 7.2b    Stream Tube

        Properties of Stream tube:

       1. The stream-tube is bounded on all sides by streamlines.

       2. Fluid velocity does not exist across a streamline, no fluid may enter or leave a stream-tube except through its ends.

       3. The entire flow in a flow field may be imagined to be composed of flows through stream-tubes arranged in some arbitrary positions.