Consider a convergent nozzle as shown in Fig.
40.7(a). Figure 40.7(b) shows the pressure ratio p/ p0 along the length of the nozzle.
The inlet conditions of the gas are at the stagnation state (p0, T0) which are constants. The pressure at the exit plane of the nozzle is denoted by PE and the back pressure is PB which can be varied by the adjustment of the valve. At the condition P0 = PE = PB there shall be no flow through the nozzle.
The pressure is P0 throughout, as shown by condition (i) in Fig. 40.7(b). As PB is gradually reduced, the flow rate shall increase. The pressure will decrease in the direction of flow as shown by condition (ii) in Fig. 40.7(b). The exit plane pressure PE shall remain equal to PB so long as the maximum discharge condition is not reached. Condition (iii) in Fig. 40.7(b) illustrates the pressure distribution in the maximum discharge situation.
When
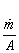
attains its maximum value, given by substituting Ma = 1 in Eq. (40.12), P
E is equal to p* . Since the nozzle does not have a diverging section, further reduction in back pressure P
B will not accelerate the flow to supersonic condition. As a result, the exit pressure P
E shall continue to remain at p * even though P
Bis lowered further.
The convergent-nozzle discharge against the variation of back pressure is shown in Fig.
40.8. We are aware, that the maximum value of (m/A) at Ma = 1 is stated as the choked flow. With a given nozzle, the flow rate cannot be increased further. Thus neither the nozzle exit pressure, nor the mass flow rate are affected by lowering PB below p *.