Isentropic Flow in a Converging Nozzle
Consider the mass flow rate of an ideal gas through a converging nozzle. If the flow is isentropic, we can write
where 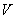 is flow velocity, is flow velocity, 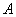 is area, is area, 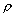 is the density of the field. is the density of the field.
This can equivalently be written as-
In the expression (40.12), 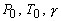 and R are constant and R are constant
-
The discharge per unit area
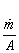 is a function of Ma only. There exists a particular value of Ma for which it is maximum. Differentiating with respect to Ma and equating it to zero, we get
Hence, discharge is maximum when Ma = 1.
-
We know that
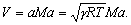 . By logarithmic differentiation, we get
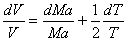 |
(40.13) |
By logarithmic differentiation, we get
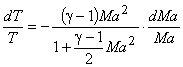
|
(40.14) |
From Eqs(40.13) and (40.14) , we get
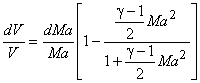 |
|
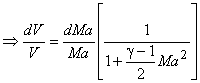 |
(40.15) |
From Eqs (40.11) and (40.15), we get
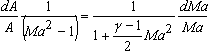 |
|
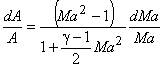 |
(40.16) |
By substituting Ma=1 in Eq. (40.16), we get dA = 0 or A = constant.
-
Ma=1 can occur only at the throat and nowhere else, and this happens only when the discharge is maximum. When Ma = 1 , the discharge is maximum and the nozzle is said to be choked.
The properties at the throat are termed as critical properties which are already expressed through Eq. (40.6a), (40.6b) and (40.6c). By substituting Ma = 1 in Eq. (40.12), we get
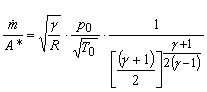 |
(40.17) |
(as we have earlier designated critical or sonic conditions by a superscript asterisk). Dividing Eq. (40.17) by Eq. (40.12) we obtain
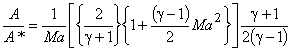 |
(40.18) |
From Eq. (40.18) we see that a choice of Ma gives a unique value of A/A* . The following figure shows variation of A / A * with Ma (Fig 40.6). Note that the curve is double valued; that is, for a given value of A/A* (other than unity), there are two possible values of Mach number. This signifies the fact that the supersonic nozzle is diverging.
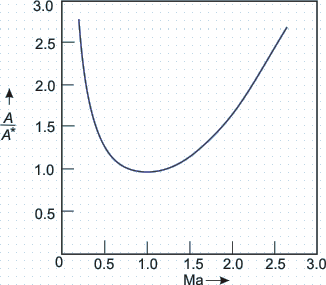
Fig 40.6: Variation of A/A* with Ma in isentropic flow for
 = 1.4 = 1.4
The area ratio, as a function of Mach number, is also included in the Isentropic Table (see Spruk [1], Muralidhar and Biswas [2].
|