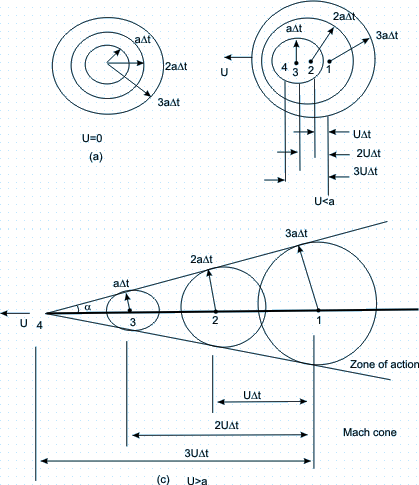
Consider a point source emanating infinitesimal pressure disturbances in a still fluid, in which the speed of sound is "a". If the point disturbance, is stationary then the wave fronts are concentric spheres. As shown in Fig. 39.2(a), wave fronts are present at intervals of Δt .
Now suppose that source moves to the left at speed
U < a. Figure 39.2(b) shows four locations of the source, 1 to 4, at equal intervals of time
, with point 4 being the current location of the source.
When the source speed is supersonic U > a (Fig. 39.2(c)), the point source is ahead of the disturbance and an observer in the downstream location is unaware of the approaching source. The disturbance emitted at different
 , with point 4 being the current location of the source.
, with point 4 being the current location of the source. 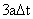 in an interval of time
3Δt . During this time the source has moved to the location 4 at a distance of
3uΔt from point 1. The figure also shows the locations of the wave fronts emitted while the source was at points 2 and 3, respectively.
in an interval of time
3Δt . During this time the source has moved to the location 4 at a distance of
3uΔt from point 1. The figure also shows the locations of the wave fronts emitted while the source was at points 2 and 3, respectively.
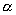 , is known as Mach angle and given by
, is known as Mach angle and given by