This shows that
(a)
 if
dρ is positive. if
dρ is positive.
(b) A compression wave leaves behind a fluid moving in the direction of the wave (Fig. 39.1(a)).
(c) Equation (39.1) also signifies that the fluid velocity on the right is much smaller than the wave speed " a ". Within the framework of infinitesimal strength of the wave (sound wave), this " a " itself is very small.
- Applying the momentum balance on the same control volume in Fig. 39.1 (b). It says that the net force in the x direction on the control volume equals the rate of outflow of x momentum minus the rate of inflow of x momentum. In symbolic form, this yields
In the above expression, Aρa is the mass flow rate. The first term on the right hand side represents the rate of outflow of x-momentum and the second term represents the rate of inflow of x momentum.
- Simplifying the momentum equation, we get
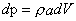 |
(39.2) |
If the wave strength is very small, the pressure change is small.
Combining Eqs (39.1) and (39.2), we get
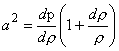 |
(39.3a) |
The larger the strength
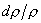 of the wave ,the faster the wave speed; i.e., powerful explosion waves move much faster than sound waves.In the limit of infinitesimally small strength, of the wave ,the faster the wave speed; i.e., powerful explosion waves move much faster than sound waves.In the limit of infinitesimally small strength,
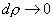 we can write we can write
 |
(39.3b) |
Note that
(a) In the limit of infinitesimally strength of sound wave, there are no velocity gradients on either side of the wave. Therefore, the frictional effects (irreversible) are confined to the interior of the wave.
(b) Moreover, the entire process of sound wave propagation is adiabatic because there is no temperature gradient except inside the wave itself.
(c) So, for sound waves, we can see that the process is reversible adiabatic or isentropic.
So the correct expression for the sound speed is
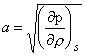 |
(39.4) |
For a perfect gas, by using of
 , and , and
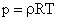 , we deduce the speed of sound as , we deduce the speed of sound as
 |
(39.5) |
For air at sea-level and at a temperature of 150C, a=340 m/s
|