|
Pipe Network: Solution by Hardy Cross Method
- The distribution of water supply in practice is often made through a pipe network comprising a combination of pipes in series and parallel. The flow distribution in a pipe network is determined from Eqs(36.9) and (36.10).
- The solution of Eqs (36.9) and (36.10) for the purpose is based on an iterative technique with an initial guess in Q
- The method was proposed by Hardy-Cross and is described below:
- The flow rates in each pipe are assumed so that the continuity (Eq. 36.9) at each node is satisfied. Usually the flow rate is assumed more for smaller values of resistance R and vice versa.
- If the assumed values of flow rates are not correct, the pressure equation Eq. (36.10) will not be satisfied. The flow rate is then altered based on the error in satisfying the Eq. (36.10).
- Let Q0 be the correct flow in a path whereas the assumed flow be Q. The error dQ in flow is then defined as
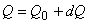 |
(36.11) |
Let 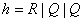 |
(36.12a) |
and 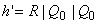 |
(36.12b) |
Then according to Eq. (36.10)
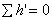 in a loop in a loop |
(36.13a) |
and 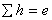 in a loop in a loop |
(36.13b) |
Where 'e' is defined to be the error in pressure equation for a loop with the assumed values of flow rate in each path.
From Eqs (36.13a) and (36.13b) we have
or, 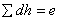 |
(36.14) |
Where dh (= h - h' ) is the error in pressure equation for a path. Again from Eq. (36.12a), we can write
or, 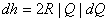 |
(36.15) |
Substituting the value of dh from Eq. (36.15) in Eq. (36.14) we have
Considering the error dQ to be the same for all hydraulic paths in a loop, we can write
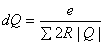 |
(36.16) |
The Eq. (36.16) can be written with the help of Eqs (36.12a) and (36.12b) as
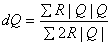 |
(36.17) |
The error in flow rate dQ is determined from Eq. (36.17) and the flow rate in each path of a loop is then altered according to Eq. (36.11).
The Hardy-Cross method can also be applied to a hydraulic circuit containing a pump or a turbine. The pressure equation (Eq. (36.10)) is only modified in consideration of a head source (pump) or a head sink (turbine) as
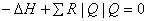 |
(36.18) |
where 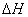 is the head delivered by a source in the circuit. Therefore, the value of is the head delivered by a source in the circuit. Therefore, the value of 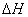 to be substituted in Eq. (36.18) will be positive for a pump and negative for a turbine. to be substituted in Eq. (36.18) will be positive for a pump and negative for a turbine.
|